When searching for subsets, the quantities that we search over are binary (i.e. the predictor is used or excluded from the model). The description above implies that the position is a real valued quantity. If the positions are centered around zero, Kennedy and Eberhart (1997) suggested using a sigmoidal function to translate this value be between zero and one. A uniform random number is used to determine the binary version of the position that is evaluated. Other strategies have been proposed, including the application of a simple threshold to the translated position (i.e. if the translated position is above 0.5, include the predictor).
R has the pso package that implements this algorithm. It does not work for discrete optimization that we need for feature selection. Since its licensed under the GPL, I took the code and removed the parts specific to real valued optimization. That code is linked that the bottom of the page. I structured it to be similar to the R code for genetic algorithms. One input into the modified pso function is a list that has modules for fitting the model, generating predictions, evaluating the fitness function and so on. I've made some changes so that each particle can return multiple values and will treat the first as the fitness function. I'll fit the same QDA model as before to the same simulated data set. First, here are the QDA functions:
qda_pso <- list(
fit = function(x, y, ...)
{
## Check to see if the subset has no members
if(ncol(x) > 0)
{
mod <- train(x, y, "qda",
metric = "ROC",
trControl = trainControl(method = "repeatedcv",
repeats = 1,
summaryFunction = twoClassSummary,
classProbs = TRUE))
} else mod <- nullModel(y = y) ## A model with no predictors
mod
},
fitness = function(object, x, y)
{
if(ncol(x) > 0)
{
testROC <- roc(y, predict(object, x, type = "prob")[,1],
levels = rev(levels(y)))
largeROC <- roc(large$Class,
predict(object,
large[,names(x),drop = FALSE],
type = "prob")[,1],
levels = rev(levels(y)))
out <- c(Resampling = caret:::getTrainPerf(object)[, "TrainROC"],
Test = as.vector(auc(testROC)),
Large_Sample = as.vector(auc(largeROC)),
Size = ncol(x))
} else {
out <- c(Resampling = .5,
Test = .5,
Large_Sample = .5,
Size = ncol(x))
print(out)
}
out
},
predict = function(object, x)
{
library(caret)
predict(object, newdata = x)
}
)
Here is the familiar code to generate the simulated data:
set.seed(468)
training <- twoClassSim( 500, noiseVars = 100,
corrVar = 100, corrValue = .75)
testing <- twoClassSim( 500, noiseVars = 100,
corrVar = 100, corrValue = .75)
large <- twoClassSim(10000, noiseVars = 100,
corrVar = 100, corrValue = .75)
realVars <- names(training)
realVars <- realVars[!grepl("(Corr)|(Noise)", realVars)]
cvIndex <- createMultiFolds(training$Class, times = 2)
ctrl <- trainControl(method = "repeatedcv",
repeats = 2,
classProbs = TRUE,
summaryFunction = twoClassSummary,
## We will parallel process within each PSO
## iteration, so don't double-up the number
## of sub-processes
allowParallel = FALSE,
index = cvIndex)
To run the optimization, the code will be similar to the GA code used in the last two posts:
set.seed(235)
psoModel <- psofs(x = training[,-ncol(training)],
y = training$Class,
iterations = 200,
functions = qda_pso,
verbose = FALSE,
## The PSO code uses foreach to parallelize
parallel = TRUE,
## These are passed to the fitness function
tx = testing[,-ncol(testing)],
ty = testing$Class)
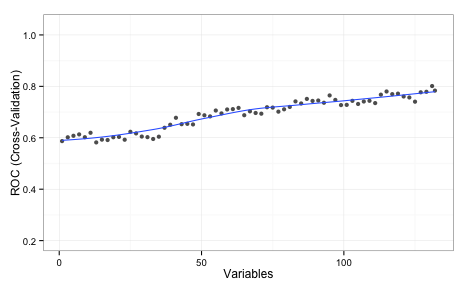
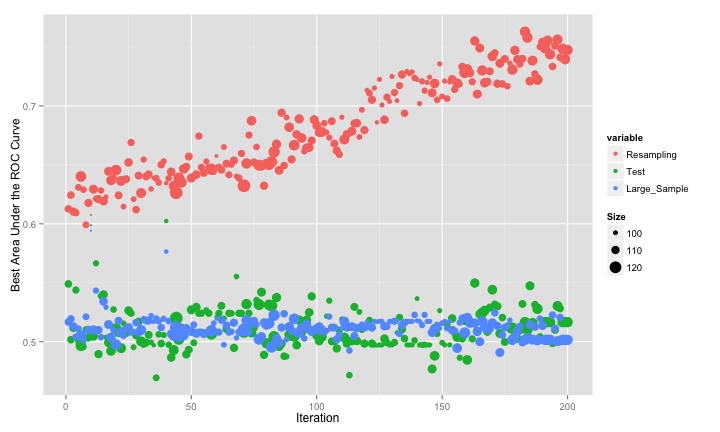
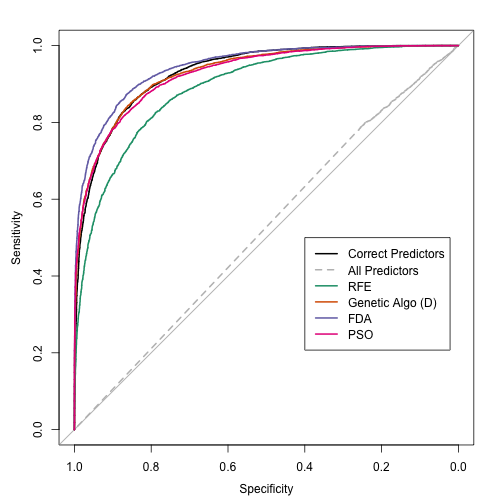
Since this is simulated data, we can evaluate how well the search went using estimates of the fitness (the area under the ROC curve) calculated using different data sets: resampling, a test set of 500 samples and large set of 10,000 samples that we use to approximate the truth.
The swarm did not consistently move to smaller subsets and, as with the original GA, it overfits to the predictors. This is demonstrated by the increase in the resampled fitness estimates and mediocre test/large sample estimates: